圏論でアハ体験 - Bug Catharsis

もう1週間以上前になりますが、Code2012という合宿イベントに参加してきました。いろいろな方との交流あり、温泉あり、クラウディアさんありと大変楽しかったので、ぜひ来年も参加したいです。

で、VBerのくせにそちらで「5分じゃわからないモナド - 圏論なんて華麗にスルー」というタイトルでLTをしてきました。なぜか、宴会の後にLTをやるという謎なタイムスケジュールとなっていたため、十分にアルコールが回った状態でお話をしました。時間通りにジャスト5分で話しきれたのは奇跡です。来年はそのあたり考慮してもらいたいかも...しれません。LTの後にいくつか質問をいただいて、モナドや圏やF#についてなんだか結構な時間追加でしゃべったような気がします。

LTの要点としましては、「モナドを使うのに圏論の知識は必要ない。」という意見はまったくそのとおりなのだけど、だからといって関数型言語を学ぶ人が圏論に触れることを無駄とは言えないということ。「プログラミングでモナドを使えるようになってから関数型言語の数学的背景であるところの圏論に触れてみることは、ぜんぜん無駄ではなかったし、むしろ思っていた以上に収穫があった！」という体験について伝えたい。「モナドは単なる自己関手の圏におけるモノイド対象だよ。」の意味を理解できるのとできないのとでは、見える景色がだいぶ違ってくる。圏論にはアハ体験があります。ある程度根気は必要だけど...ということを伝えたかったというものです。

当日話した内容とまったく同じではありませんが、大体以下のような内容でしゃべってきました。こわい人にこわいこわいされるのがこわいので、当初Webにはアップしないでおこうと考えていたのですが、いろいろと思うところが有り、思い直して現時点の自分の考えを晒しておくことにしました。かなり端折り気味な内容ですが雰囲気だけでも。

5分じゃわからないモナド - 圏論なんて華麗にスルー

5分じゃわからないモナド　始めさせていただきます。

ぜくるです。
静的型付け関数型言語が大好きです。　F#が大好きです。

美しいコードは好きですか？

もちろん大好きですよね！！！

美しいコードを書きたければ、より多くの良いコードを読まなければなりません。

ならば、関数型言語が読めないのは、あまりにも損です。

じゃいつやるか？今でしょ！

モナド。みなさん聞いたことくらいはありますよね。

モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも？

どういうことだってばよ！？

関数型言語を成り立たせている構造がそもそも圏だよ。
プログラミングとは、だいたいクライスリ圏の射を作ることらしいよ。

数学由来の抽象であるところの、代数的な構造をプログラミングに応用したらしいよ。

「モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも？」
の意味がなんでわからんのかというと、そもそも専門用語がわからんからにほかならない。

4年くらい関数型言語を勉強してきた中で、わたしがモナドをわかるまでにやったこと。

まずは具体的にモナドを使ったプログラムを書きまくります。
野性的なプログラマはだいたい体で覚えます。

慣れてくると自分で定義します。より理解が深まります。
自分で考えた新しいモナドを定義することもできるようにもなります。

モナドを使うだけなら、高度な理論は全く必要ないんです。
モナドを使いこなすのに「圏論の知識なんて必要ない」そのとおりだと思います。

でも、最小限把握しておいたほうがよい用語や概念があります。
俺達プログラマは好奇心旺盛だもんね！

少し遠回りをしてもいいんじゃないか。
モナドの数学的な背景すべてを知らなくても、おおまかに概観を把握するだけで見える景色が違ってくる。

圏論に触れてみることにしました。

とりあえず、専門書に当たってみる。今年の正月からコツコツと勉強しています。
でも、この本はジャンル的に少し偏っているし、１，２章でお腹いっぱいです。

で、気づいたのが、そもそも群の知識がないと圏論を理解するのは困難ということです。

基礎の基礎が大事です。

集合や群を理解するために、代数を勉強をします。この時点でかなり遠回り。でも、いいんです。

圏論の本にも頻出する集合や群に関する記号の意味を理解するのに役立つ。穴埋めの練習問題形式。
やさしい入門書ですが、基本的なことや記号の意味を把握するだけならこれで十分だと思いました。
でも、マグマとか半群とかモノイドの説明はないので、それらは別の書籍などで補う必要がある。
思いの他おもしろかったので、気持ちに余裕があったら高度な内容にも挑戦してみたいかも。

群と言えばガロア。置換群もプログラミングに関係が深いと感じました。
解説がわかりやすいだけではなく、数学の歴史的な背景も合わせて読めるからお得。
タイトル通り、中１でも読める内容なので安心です。でも後半は結構面倒くさいです。

代数的構造とはなんなのか。具体例を交えてわかりやすく解説してくれます。群の教科書。
こちらおすすめです。寝る前に読んだら、ぐっすり眠れます。

で、群・環・体...と、代数的構造にも色々とありますが、結局プログラミングに関係の深いのは、モノイドという構造です。
どうやら、プログラマ的には、モノイド以外の代数的構造については華麗にスルーしても問題なさそうです。

で、圏とはなんだったのか。
対象と射の集まりのことです。

ただし、ひとつの恒等射が必要。

また、合成射について、結合律を満たす必要があります。

モナド則ととっても似ていますね。
というかむしろ、モノイドの構造そのものです。

「圏」と同時に最小限知っておかなきゃなんないのが、「関手」です。
圏から圏への写像のことです。

自己関手。同一の圏から圏への関手のこと。
そのまんまですね。

Haskellプログラムは、圏（Hask圏）の中で動いています

F#のプログラムは、.NETの圏の中で動いています

どういうことなの？

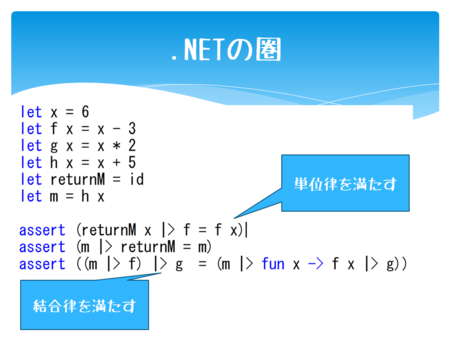
F#のコードです。FSharpxというライブラリのMaybeモナドを使ってモナド則をコードで表現してみます。

モナド則を満たすわけですから、これは単位律と結合律を満たします。

モナドを使わずに、ただの関数で同様の表現をしてみます。
恒等射はidですね。

同じく単位律と結合律を満たします。

完全に一致！！！
いずれも、圏の条件を満たしており、それぞれが圏だということがわります。

圏空気すぎワロタ

F#の世界の値と関数は、.NETの圏からMaybeモナドの圏への写像であるところの「関手」return によって、 Maybeモナドの圏の値と関数に写像することができる。
で、Maybeの圏はこのとき.NETの圏に含まれていますから、自己関手の圏になるわけですね。で、Maybeという代数的データ型はモノイドの構造を持っているモノイド対象ということですね。